时间: 2021-07-30 09:14:52 人气: 10 评论: 0
已知参与计算的各个feature,如何去确定每个feature的权重呢?本文将为大家介绍一种相对科学的办法,来处理这种多因子权重设置的问题。

数据处理领域,在进行相关指标计算的时候,一个指标通常有若干了因子(通常称之为feature,下同)参与计算,而每个因子对该指标的贡献度(通常称之为weight或contribution,下同)又不同,比如GMV,商品人气分,用户满意度等等。通常可以表示为如下公式:
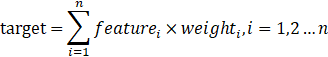
这时,我们通常遇到下面这个问题:
已知参与计算的各个feature,如何去确定每个feature的权重呢?
夏唬人目前在做电商推荐策略相关的事情,经常遇到这种问题。
比如在物品(通常称之为item,下同)召回的时候,如何对每个item进行排序呢?
比如以人气分作为排序依据,那么通常**考虑销量,评价,浏览次数,下单次数,收藏次数,加购次数等等。
如果一味的按照经验去进行初始化权重,然后不停的A/B测试、权重调整,是一件研发成本特别高的事情。
今天就给大家介绍一种相对科学的办法来处理这种多因子权重设置的问题。
简单介绍一下什么是AHP?
层次分析法,简称AHP,它是一种运筹学**。
是指将与决策总是有关的元素分解成目标、准则、方案等层次,在此基础之上进行定性和定量分析的决策方法。
“该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初,在为美国国防部研究”根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时,应用网络系统**和多目标综合评价方法,提出的一种层次权重决策分析方法。”
所以,AHP**本质是通过把一个复杂的问题拆解为多个目标或准则,并且通过定性量化的方式为每个目标进行赋权的一个过程。
简单来说AHP就是拆解加赋权,下面详细讲一下过程。
什么是判断矩阵?
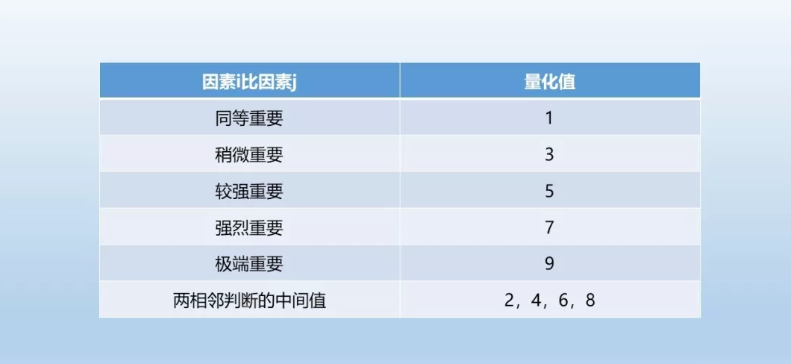
判断矩阵就是以参与指标计算的所有ferture组成的一个方阵,并且给出两两“比较量化值”。举例如下:
对于A和B两个因子,1表示:A和B一样重要;3表示:A比B重要一些;5表示:A比B重要;7表示:A比B重要的多;9表示:A比B极其重要,具体标准如下图所示:
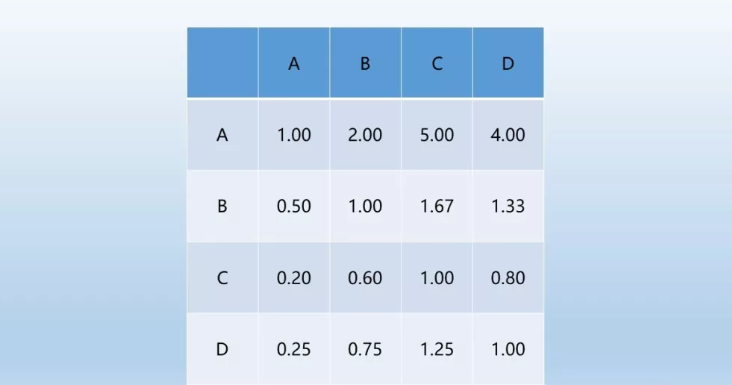
这其实就是一个典型的小组投票的过程,通过在方阵行列元素的两两比较,最终可以生成一个判断矩阵。比如对于有A,B,C,D四个feature的判断矩阵如下图所示:
所谓一致性校验是指在进行投票的时候的公平性和一致性。
比如你认为A比B重要,B比C重要,但是从最后的结果来看是C比A重要,这样即为不一致。
一致性校验是通过计算校验系数来实现的,通常用CR来表示,小于0.1即表示一致性校验通过。
CR包含一致性指标(CI)和随机一致性指标(RI)两部分,CR=CI/RI。
CI和RI是一个固定值,与矩阵的阶数有关。
剩下的是一个比较复杂的数学过程,简单介绍几个概念,计算过程大家可以百度一下即可。
下图是通过excel进行计算的:
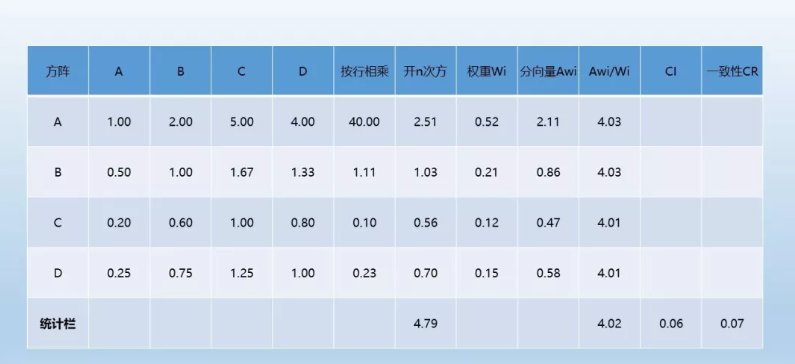
通过进行小组投票和自动计算,最终CR的值为0.06,因此一致性检验通过。
权重Wi列即为每个feature的权重,因此最终我们可以得出该指标的计算公式为:
![]()
完美解决!
大家这里或许**有个疑问:
采用AHP的方法进行赋权,小组投票阶段是主观判断重要性的,所以是不是**带来误差?
**,一定**。
不过还是我之前说的,策略一定是建立在业务之上的,撇开业务谈策略都是伪策略。
采用AHP模型进行多因子赋权,
需要对该业务有足够的了解,更需要对该target下的多个feature有足够的了解,哪个对于target的贡献度是最大的。
比如对于一个商品,什么样的商品是用户喜欢的?用户喜欢的商品有哪些feature?每个feature对于用户喜欢的贡献程度是什么样的?这些都是需要业务经验参与的。
如果说科学的方法都有一个前提假设,那么AHP也有一个前提,就是先了解业务,再谈策略。
以上,希望能帮助到大家。
作者:夏唬人。公众号:夏唬人,某厂推荐策略产品经理。
本文由 @夏唬人 原创发布于人人都是产品经理。未经许可,禁止转载
题图来自Unsplash,基于CC0协议