时间: 2021-07-30 09:18:41 人气: 15 评论: 0

因子分析主要用于分析商户O2O运营数据,了解商家的行为信息,找出数据背后的共性,最终对商家进行综合评价,挖掘商家特点。
获得企业所属的商户O2O运营数据后,通过分析它们在一段时间内的线上线下行为信息,找出这些变量的共性,降低分析维度,对商户进行综合评价,可以知道产品运营效果是否达到预期。
因子分析(探索结构,简化数据,综合评价)
SPSS(数据分析的重量级应用,与SAS二选一)
实例:100个商户的O2O运营数据
不瞎逼逼,直接开干。


【描述】
勾选“KOM和巴特利特球形度检验”,目的是用于生成检验因子分析适合度的统计指标。

【提取】
方法选择“主成分”,这是最常用的提取因子的方法;
勾选“碎石图”,用于辅助判断因子个数。

【旋转】
选择“最大方差法”,用于更好的解释因子所包含的意义。
最大方差法师最常用的,该方法能够使每个变量尽可能的在一个引子上有较高的载荷,在其余因子上载荷较低,从而方便对因子进行解释。

【得分】
勾选“保存为变量”,方法选择“回归”,用于保存计算的到的因子得分。

【选项】
勾选系数显示格式中的“按大小排序”,是为了让系数大小有序,方便观察;勾选“排除小系数”,输入0.4,这样在结果中相关系数小于0.4的**被排除,不再显示,也是为了方便观察(因为我们是寻找相关系数高的)
注意:这里不必生搬硬套,也不必也定时0.4,可视具体情况而定
分析结果解读:

该结果主要用来检验数据是否适合因子分析,主要参考KMO统计量即可。
KMO统计量为0.627,大于0.5小于0.7,尚可以接受因子分析。

这个结果是“变量共同度”,显示了原始变量能被提取的因子解释的程度。
本例中所有变量共同度都在60%以上,可以认为所提取的因子对各变量的解释能力是可以接受的。

该图是“总方差解释”,显示了通过分析所提起的因子数量,以及所提取的因子对所有变量的累计方差贡献率。
累计方差贡献率大于60%,则说明因子对变量的解释能力尚可接受,达到80%,说明因子对变量的解释能力非常好。
本例根据“初始特征值”大于1的标准提取了两个因子,旋转之后累计方差贡献率达到72.367%,因子的解释能力较好。

碎石图”能辅助我们判断最佳因子个数,通常是选区取现中比较陡峭的位置所对应的因子个数。
本例前三个音字都在较陡峭的曲线上,所以提取2~~3个因子都可以对原始变量有较好的解释。
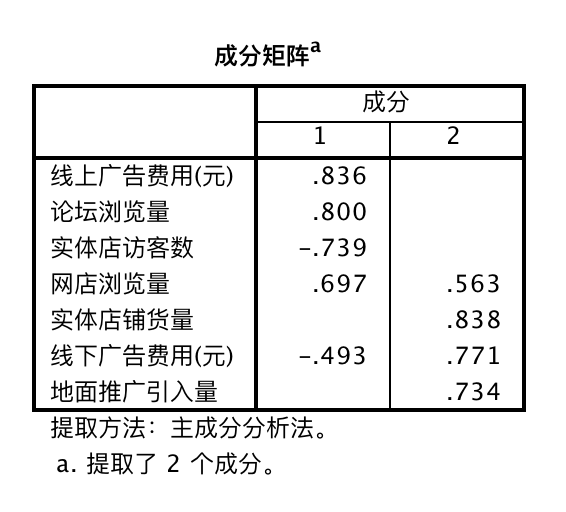
这是旋转之前的因子载荷矩阵,难以对因子进行明确定义,可以忽略不看,直接看旋转后的因子载荷矩阵。
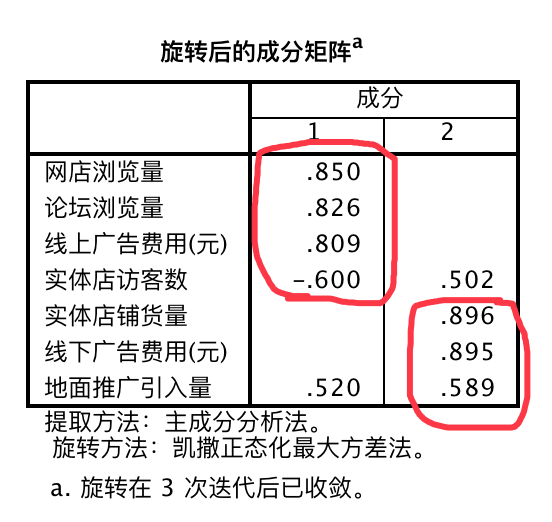
“旋转后的成分矩阵”显示的是旋转后的因子载荷矩阵,这个结果能够凸显因子含义。
第一个因子:载荷较大的变量是“网店浏览量”、“论坛浏览量”、“线上广告费用”、“实体店访客数”,说明这四个变量与该因子的相关程度较高,其中前三个是反映的是线上数据,“实体店访客数”放映的虽然是线下数据,但是与第一个因子呈现反向关系。综上所述可以吧第一个因子命名为“线上商务”。
第二个因子:载荷较大的是“实体店铺货数”、“线下广告费用”、“地面推广引入量”,说明这个变量与因子的先关程度较高,并且反映的都是线下情况。综上所述可以命名为“线下商务”。
注意:系数是按我们设置的降序排列,并且有的为空,是因为我们设置的排除小于0.4的系数是因子结果更加清晰,可读。

这个图没什么卵用,忽略不计。

新生成了两个变量就是每个商户在两个因子上的得分:第一个因子的得分,第二个因子的得分。
下面我们计算综合得分。
公式:第一个因子占的加权比重数*第一个因子得分+第二个因子占的加权比重数*第二个因子得分
本例中旋转后的方差解释图知:
因子1贡献率为38.968%,因子2贡献率为33.399,累积贡献率为72.367
所以因子1占的加权比重数=38.968/72.367
因子2所占的加权比重数=33.399/72.367


对综合得分进行将序排列,就能知道哪些商户在O2O的运营方式下表现优异。

知道了那些商家表现优异,那些商户表现比较差,就可以进行后的详细分析,以提升企业的商业价值,达到某些商业目的。
作者:膝盖哥,是一枚“跪着提需求”的产品经理。常说“不用不用,真的不用了,我跪着就好!”
本文由 @膝盖哥 原创发布于人人都是产品经理。未经许可,禁止转载。