时间: 2021-07-30 10:58:02 人气: 12 评论: 0

当你看了一部电影,但是对豆瓣的评分并不认可,知道这是为什么吗?
不知道大家有没有这样的经历 —— 看了一部电影,但对豆瓣的评分并不认可。
比如,之前看西游伏妖篇,我就很疑惑,为什么分数这么低?毕竟,周星驰是我很喜欢的导演。

而且,评论区也出现了截然相反的评价:

再比如最近的神奇女侠 Wonder Woman,虽然分数不错,但我并不觉得很好看。
此外,一直以来也有“爱乐之城/摔跤吧爸爸评分偏高了吗?”等类似的问题。所以,**想问 ——为什么有的电影分数高/低,但是我们并不认同?是不是豆瓣电影的分数有问题?
之前,从国内外评价差异(和IMDB比较)的角度分析过,比如赤壁/让子弹飞,国内外的评价并不一致,但还有没有别的原因?
选取2008-2017, 国内公映的电影。限制豆瓣评分人数在2W以上,一方面讨论大家较为熟悉、主流的电影,另一方面也尽量减少水军等的影响。总共815部电影,评分分布如图:
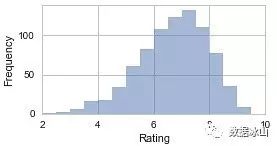
包括了很多大家熟悉的电影:

仔细观察西游的评分,**发现和相同评分的电影(杜拉拉升职记)的分布差别很大。

两者评分相同,评价人数也很多(20W, 17W),但5星和1星的比例差别很大[1]。
什么意思呢?
也就是说,尽管两者(平均)分数相同,但是背后的看法非常不同,评分差异很大,这也正好对应了上面,西游出现两种截然相反的热评的情况。
评分分布的差异,可以用方差来衡量,计算方法如下:

也就是计算 评分偏离平均分的程度 [2]。下文使用标准差(STD),方差开方即可。可以做出标准差(STD) – 豆瓣评分(Rating )散点分布图[3]。为了便于比较,做标准差97%范围线。
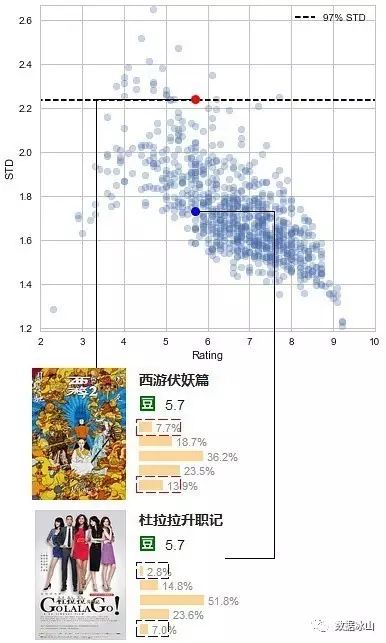
可以看到西游和杜拉拉升职记的STD差别确实很大,西游的标准差排在前3% ,争议性是巨大的,而杜拉拉则小很多。 另外,还发现散点图的有两个特点
对于收敛,可以从平均分怎么计算出来的角度理解:平均分越高,占高分的比例越大,因此评分差异较小。至于不对称,后面再说。
这里,可以看到很多典型评价差异很大的电影,比如刺客聂隐娘,一步之遥 等等都在这张图的上方,STD很高。

可以拿他们和STD较低的电影比较:

这里可以问一个问题 —— 这些电影的分数相同,但同样好看/不好看吗?
比如,刺客聂隐娘和我11的分数一样,但他们一样好看吗?
显然不是。
和前面的比较类似,刺客聂隐娘虽然评分较高,但其5星/1星和我11差别很大。为什么呢?大家可能早有耳闻,看评论,也能看到。

可能的原因,是刺客聂隐娘画面极具美感,但另一方面,剧情却让人看不懂。所以评分上出现了较大的分歧。一步之遥也是类似,算是比较有名的例子了。
而爸爸去哪儿,也能从评论中看到一些端倪:

可能的原因是,一方面是娱乐性优秀,带着小孩看电影的家长观众们觉得很好,另一方面,有人觉得这不是电影,纯属圈钱。
通常,我们总是在讨论一部电影评分的高低,但这只是平均分,当大家看法一致的时候,这个分数**很有参考价值。但当评分差异很大(STD很大)的时候,这个分数的作用就有限了。
从评分的分布,很容易想到关于评分形状的段子:

那么,电影的评分,**有多少种形状呢?
可以用K-Means来做,输入数据为5个评分等级的比例。实际可以把类别分得很细,这里简单分成6种,比较有代表性,结果如下图:

这些分布,相当于电影评分的典型形状,两头和中间对应了大家熟知的P, b和钟形分布[4]。需要注意的是,高STD的电影因为其形状差异很大,并不适用于这个分类。
这可以部分解释,为什么散点图是非对称的 —— 因为有很多4星为主的电影,但很少有2星为主的电影。毕竟,大多时候给的评价都是一般(3星),或烂**(1星),很少**有电影“精确烂到2星”。
每个形状下,也能看到STD高/低的电影,比如魔兽,爱乐之城等等。


依然可以问这个问题 —— 这些电影分数相同,但是同样好看吗?
像爱乐之城, 虽然评分和萨利机长一样,都算典型的好电影了,但是打5星的明显比萨利机长多,也侧面说明了为什么有人疑惑其分数“是否偏高”。魔兽,则可能有粉丝加成的影响。其他电影不再具体讨论,大家可以自己分析~
还有一些奇怪形状的电影,比如人间·小团圆,小时代4, 长城,并不属于上述任何一种典型分布

这是为什么?
具体原因不得而知。但实际上,这是典型的混合分布的特征,也就是说,由几个分布叠加得到。
如果把最差评分和中等评分混合起来(各按50%算),可以得到和上面非常相似的形状。

那么,有没有可能真的是混合分布呢?
查看评论,不难发现,对于人间·小团圆,是ZZ因素导致了对其评分的极大差别。
小时代可能也是类似。有人看到郭小四就要打一星,另一方面,原著粉们则表示还算不错。
那么长城呢?可以查看近期的评价。需要注意的是,这时不太可能有水军了,因为这时候的分数对票房毫无意义。简单看一下前两页,发现2-3星居多。

和当初的差评还是有差距的。更靠谱的当然是抓数据,不过豆瓣官方并没有公开相关的数据,这个以后有机**再补吧~ 延伸出来的问题是,恶评如流的电影,在下映之后,还**有那么多差评吗?
本文主要做了两件微小的工作:
回到我们最开始的问题 —— 为什么有的电影分数高/低,但是我们并不觉得如此?是分数有问题吗 ?
原因在于,那只是个平均分而已
而有意思的也在于此 —— 大多数人在谈论豆瓣的评分的时候,都知道这是平均分,也都能看到分数的分布情况。而且大多数时候,这个平均分是有效的,因为大家的评价较为接近(STD较小)
但是,很少有人注意到评分的分歧大小(即STD的大小)。所以,当看到一部STD很大的电影,平均分和我们感受不符时,我们疑惑了,进而觉得豆瓣的评分有问题。实际上,只是因为人们的评价差异太大(STD太大),使平均分的意义变得比较有限了而已。
最后,我在想,有没有可能给豆瓣评分旁边加上一个小标签?比如,对STD特别大的电影,在旁边加个“分歧警告”标签,注明 “这部电影的评价差异水平达到了前3%,平均分的参考意义较为有限”,进一步还可以分开展示好评/差评,向用户解释评价差异具体如何。这样或许能减少一些人们对(平均)评分的疑虑。
然后,分析有什么疏漏或者没讲清楚的地方,也欢迎大家指出~
[1] 这里采用的是豆瓣的评分柱状图,画法并不标准(占比最大为定宽),但适用于基本的比较
[2] **上,ordinal data不适于计算均值、方差,可见 Recommender Systems: We’re doing it (all) wrong Calculate mean of ordinal variable 。不过,算均值固然不严谨,但是更好的做法,应该是转换成一个可以量化的值,比如考虑每个值之间不同的distance, 而不是全**否定。简单起见,本文直接当作离散值计算均值、方差。
另外,豆瓣/IMDB的分数并不是简单的平均值,不过实际区别很小。但无论是众数/中位数/加权平均,都没有太大影响。因为本文讨论的是,“当用一个分数来代表电影的水平时,什么时候这个分数是有效的,什么时候是无效的?” 无论这个分数的算法如何,都**存在失效的时候(即分歧较大时)。
[3] 实际STD的尺度没有这么大。这样画图类似于把STD做规整化,更方便于比较。
[4] **上可构成的形状要更多,比如5星/1星各占50%的凹形,但这些形状在实际数据中并不存在,所以得到的聚类结果中也没有这些形状。
文中涉及的交互式散点图: cdn.rawgit.com/cqcn1991
作者:数据冰山
来自:微信公众号:数据冰山
本文由 @数据冰山 授权发布于人人都是产品经理。未经作者许可,禁止转载。
题图来自PEXELS,基于CC0协议