时间: 2021-07-30 11:08:06 人气: 38 评论: 0
在用户研究中,对于用户群选取样本量进行分析是一项很重要的工作。对于调研样本量的选取背后也有很大的学问,是不是样本量越大就越有可信度呢?可用性测试到底多少人才是最恰当的呢?这些都是用户研究调研中应该注意的问题。

用研工作中我们经常跟同事(非用研)说XX的样本量就够了,可是为什么呢?
如何决定样本量,其实是一个老生常谈的话题了,也有很多相关介绍文章。但是翻看相关文章后,就**发现介绍选多少合适的挺多的,而介绍为什么这么选就合适的却比较少。
相信很多用研同学都听过或就对其他人说过这句著名的话:
“根据尼尔森关于可用性测试的经典**,6-8人便可以找到产品80%以上的可用性问题。”
但是……为啥呢?
当有“无知的”地球人问:为什么6-8人就能发现80%以上的问题时,难道我们要理直气壮的说:“因为是尼尔森就是说的么……”
在样本量选择上,似乎有一些“约定俗成”的规定,比如:可用性测试5-8人,问卷调研大约200-500份等等……
但是,当需要和地球人**时,单单的“约定俗成”却没有足够的说服力。不如让我们一起来看看这些“约定俗成”背后的科学道理,让自己更有底气。
俗话说“8个用户可以发现80%的问题”,其实这句话并不完整,完整的说法应该是:“8个人可以80%的概率发现发生可能性大于18%的问题。”
这话太绕了,尝试用人话解释一下:如果某个APP中存在一个BUG,100个人用,50个人用都**遇到,那么我们至少有80%的可能性发现。只要可能遇到的人大于18个(发生可能性大于18%),我们都至少有80%的可能性发现。但如果这个BUG只有5个人可**遇到,那么能发现的概率就要低于80%了。
之所以这么说,背后的原理是这样一个公式:
(P(X≥1)是在n次尝试中事件至少发生1次的概率,p是某事件的概率)
前辈们根据这个公式总结出了下表:
资料来源:《用户体验度量》Jeff Sauro,James R.Lewis著,机械工业出版社。
P134-135从表中可以看出:决定样本量涉及到两个因素:一个是确定程度,一个是问题发生的概率。
再来具体看一看我们常说的“8个人”:
当选择8个人进行测试时,可以100%发现发生概率大于50%的问题,90%的可能性发现发生概率大于25%的问题,73%的可能性发现发生概率大于15%的问题。
就好像天气预报员说:100%的确定明天的降水概率大于50%,90%的确定明天的降水概率大于25%。
等等,这样的话**不**被质疑:8个人只能90%发现发生概率大于25%的问题,那发生概率低于25%的问题怎么办?就不重要了么?
不我们再来看看尼尔森介绍的一个关于钓鱼的比喻:
假设你有好多个池塘可以钓鱼,一些鱼比另一些鱼更容易抓到。
所以,如果你有10小时,你**花10个小时都在一个池塘里钓鱼,还是花5个小时在一个池塘上、花另外的5个小时在另一个池塘上呢?
为使抓到的鱼数量最大化,你应该在两个池塘上都花一些时间,以便从每个池塘里都钓到容易钓的鱼。
一次何必找那么多用户,少做几个用户先把发生率高的问题解决了,版本更新以后再继续找用户去解决发生率高的问题,省时省力效果佳。
这样基本上就可以完整的证明我们可用性测试做5-8个人就基本可以的观点了。
在做问卷调研的时候,如何估计样本量?
——众所周知有一个公式:
但是,这个公式存在一个问题:我要是连总体方差(CV2)都能知道,还做个毛线调研。
如果想估算总体方差,需要先选取一批人进行测试,得到一个样本方差,用样本方差代替总体方差,这在现实工作中显然难以实现。
于是为了便于计算,伟大的前辈对公式进行了转换:
资料来源:《社**研究方法》仇立平著,重庆大学出版社,P137作者说这一转换是根据“推论总体比例或百分比的原理”进行的。
姑且不去管这个转换原理是什么,这个公式我们可以这样来理解:当p=0.5的时候,总体的差异性最大。因为p=0.5表示两种情况出现的概率是相等的,比如:一个群体中男生和女生出现的概率都是0.5,说明男女人数相等。这种情况下,这个群体的性别差异是最大的。
由于总体差异越大,需要的样本量就越大。我们面对任何总体的时候,都可以假设“这是一个差异性最大的总体”,来计算我们所需要的样本量。因此,把p=0.5代入,就简化出了一个可以供我们轻松计算样本量的公式。
如果想看到总体不同差异所对应的样本量,前人还总结了这样一个表:
资料来源:《社**研究方法》仇立平著,重庆大学出版社,P137
因此假设总体差异性最大的情况下,在习惯使用的5%误差档,300多的样本也就可以了。
当然,在具体使用过程中,并不用查表那么麻烦。有一个著名的计算样本量的网站,直接去算就OK了。
首先,总体规模**对样本量有影响。当总体规模比较小的时候,对样本量影响较大。但是当总体规模达到一定程度以后,对样本量增加的需求是较小的。
我们往往调查所涉及到的总体不是无限总体,产品的用户人数都是一个有限的数量。因此,在计算所需样本量的时候,为了更精确可以加入变量“总体规模”,公式大概长成这个样子:
然而,这不是重点,重点是通过这个公式可以计算出,不同总体规模所需要的样本量大致如下:
由此可以看出:当总体规模在1万以下时,随着总体规模上升,所需样本量增加比较大。但是,当总体规模在1万以上时,规模再变大,所需样本人数的增长变得缓慢。
为了得到更准确的答案,我们不妨用计算样本量的网址自己来算一下。
假设置信区间为±5个标准差。计算结果如下:
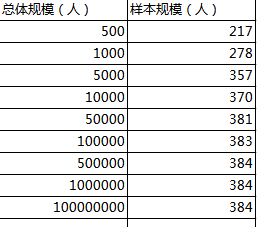
如果再有人说:我们是亿级的产品,1000人怎么能代表我们的用户?
就可以理直气壮的告诉他:“总体规模10万以上和10万所需要的样本量并没有什么区别呢。”
样本量选多少合适,对于调研本身而言或许不是个问题。但是,当我们想推动调研结果的时候,样本量却很容易遭到对方质疑。
可能是几百个人的答案看起来容易让人觉得不靠谱,也可能因为样本量是最容易质疑的一个因素……
无论如何,多了解一些背后的原因,让自己更有底气,或许才能更好地说服别人。
原作者:陈聆帙@NetEase电商设计中心 ,笔者根据自己工作需要部分内容稍作调整。欢迎交流!
本文由 @黑眼镜的猫 发布于人人都是产品经理。未经许可,禁止转载
题图来自Unsplash,基于CC0协议